在前面我們實作了 Linear Regression、多變數的 Linear Regression 以及 Logistic Regression。在這些實作的過程當中我們都僅僅只是用最簡單的 case 去實作,不過往往在實務上你會面臨到許多的問題。接下來希望透過一些實例帶出在訓練模型的過程中你也許會面臨的問題,以及這些問題應該如何解決。
首先要來看的是 過擬合 Overfitting 問題。
還記得在過去討論模型時我們選擇的都是極簡單的模型,方便我們先快速理解每個問題的解決方案與實作細節。不過當我們選擇更加複雜的模型時,往往會使得你的模型 過分貼合訓練資料 。
嗯?這樣不是很好嗎?
我們訓練模型的目的不就是希望讓模型的準確度越高越好,最好是 100% 正確,那我就可以宣稱我的模型什麼都知道,在這個問題上它是個絕對的專家了嗎?
實際上現實生活當中的問題並不是這樣的,更多時候我們的資料當中充滿了噪點與誤差,或是我們擁有的參數還不夠多,導致你其實無法做到 100% 的準確。
舉例來說,在預測房價時也許屋齡會是個影響因素吧!雖然大多時候屋齡越高也就意味著這個房子的屋況越糟,但卻也不盡然。甚至有許多時候人們會更傾向買老房子。
我們要的不是絕對的準確,而是即便存在例外狀況,機器仍然能有一定的預測水準。
讓我們來看一個 Linear Regression 的例子。
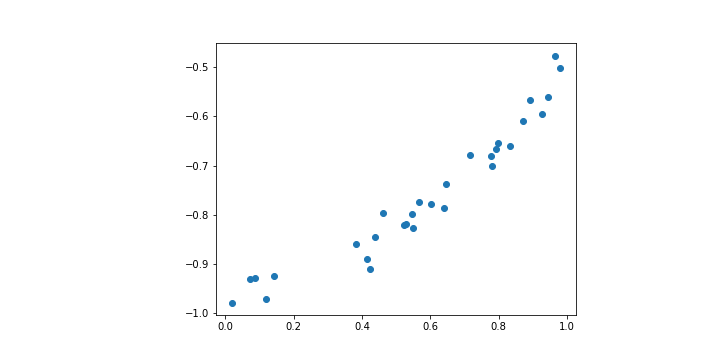
上面這張圖其實是透過 sin 函數加上一點噪點產生的圖形。也就是說理想狀況下我們會希望模型最終產生的結果能夠比較貼近 sin 函數。
def real_func(x):
return np.sin(1.5 * np.pi + x)
n_samples = 30
np.random.seed(0)
x = np.random.rand(n_samples)
y = real_func(x) + np.random.rand(n_samples) * 0.1 # 加上 noise
現在我們嘗試使用幾種不同 degree 的多項式來試圖貼近這樣的函數看看。這裡選擇了三種多項式。
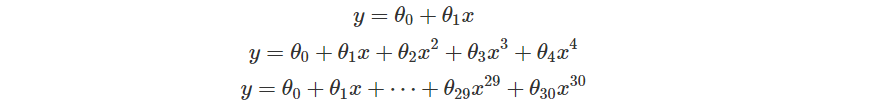
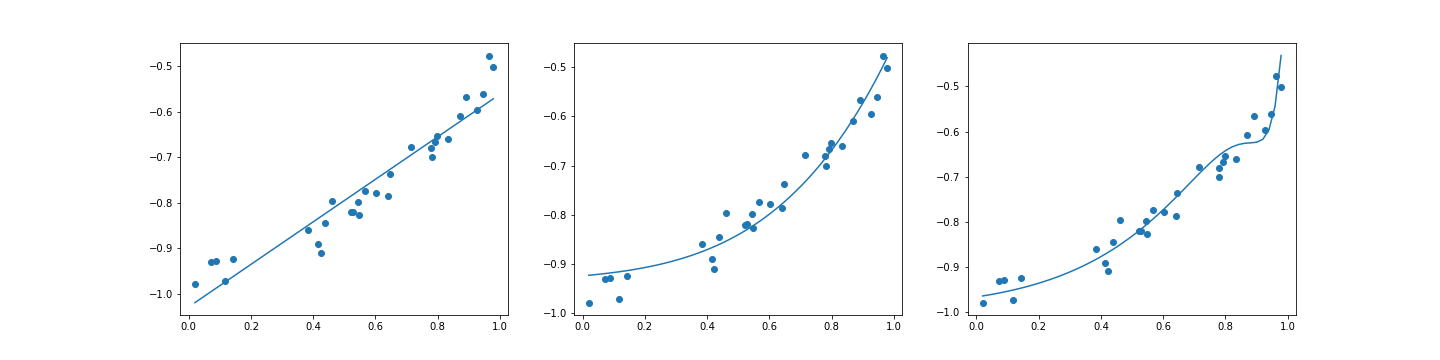
接下來就透過過去 Linear Regression 的方法,試著找出這些參數 。底下是三個模型依序得到的結果。
更新的過程大致上是這樣的
| Degree = 1 | Degree = 4 | Degree = 30 |
|---|---|---|
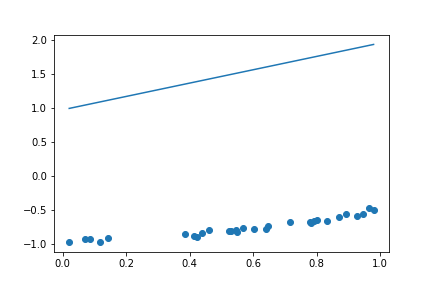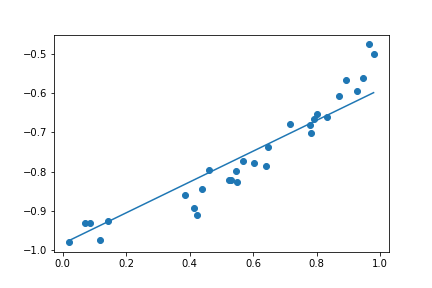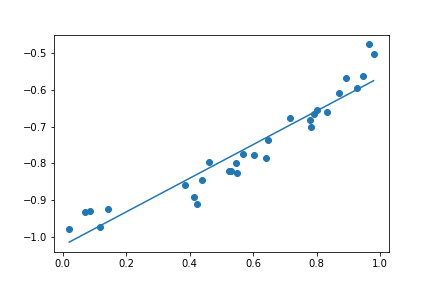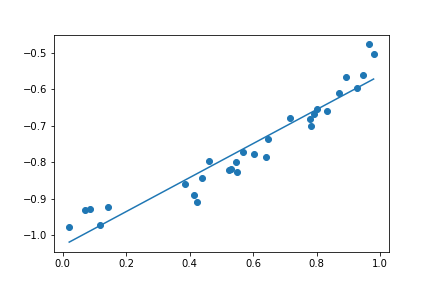 |
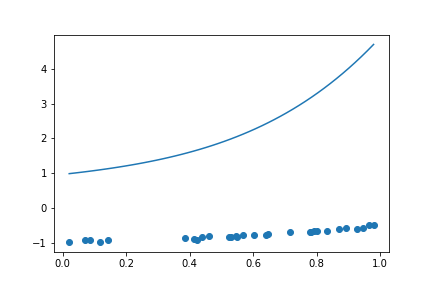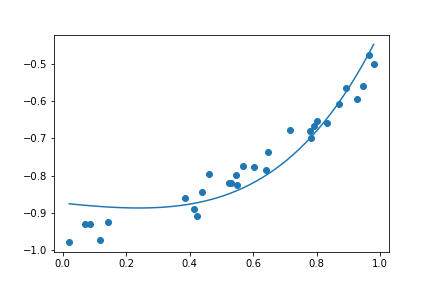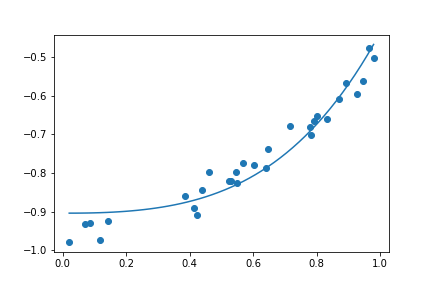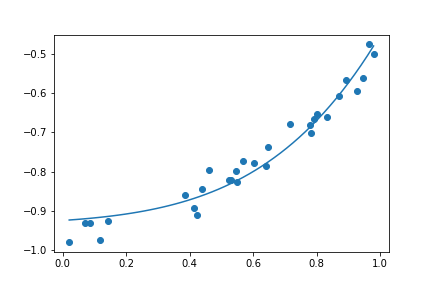 |
 |
這三種結果的 Loss 其實都很低
| Degree = 1 | Degree = 4 | Degree = 30 |
|---|---|---|
| 0.0008686038257840846 | 0.00044516618684058585 | 0.0004638278131780861 |
如果單看 Loss 的話,這三種其實都很棒,但是當我們拉回現實,也就是 這個函數,你會發現這三個函數 degree 越高,誤差越糟糕。
我們取 這個範圍,取 50 個 sample 點,去分別計算這三個模型的 Loss 大小。
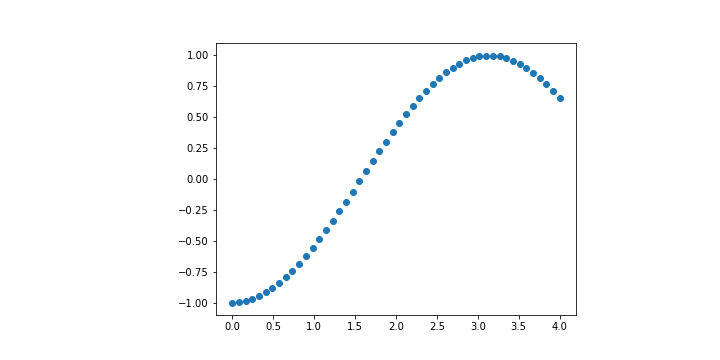
| Degree = 1 | Degree = 4 | Degree = 30 |
|---|---|---|
| 0.12824792221185963 | 262.9516729395171 | 1.6317728996135443e+33 |
這也就是 overfitting 的樣子。也許這三個函數在訓練資料上做得很棒,但 那也僅限於訓練資料 。一將情況拉回現實之後得到的會是慘不忍睹的結果。
不僅僅是在 Linear Regression,在 Logistic Regression 或是其他 Machine Learning 的問題往往都會有 Overfitting 的可能。
如果你好奇上面的 code 怎麼寫的,可以參考我的 Github
造成 Overfitting 的原因可能有下列幾種
較為常見的四種原因有這幾種,當然隨著更多技巧出現,這些技巧也有可能引申出 Overfitting 的問題,不過現階段我們先認識到這四種原因是造成 Overfitting 的常見原因即可。
好,我們知道 Overfitting 是個問題了,但是如果我只是看 Loss 的話,前面這三種模型我都認為他們做得很棒,那我應該要如何偵測 Overfitting?
前面我們在舉例的時候驗證 Overfitting 出現的方法很簡單,就是透過 真實的資料 來告訴你你的模型有多糟。類似的想法,更多時候我們在訓練一個模型的時候並不會直接把全部的資料拿進去訓練,而是切成 Training Data 以及 Test Data 。
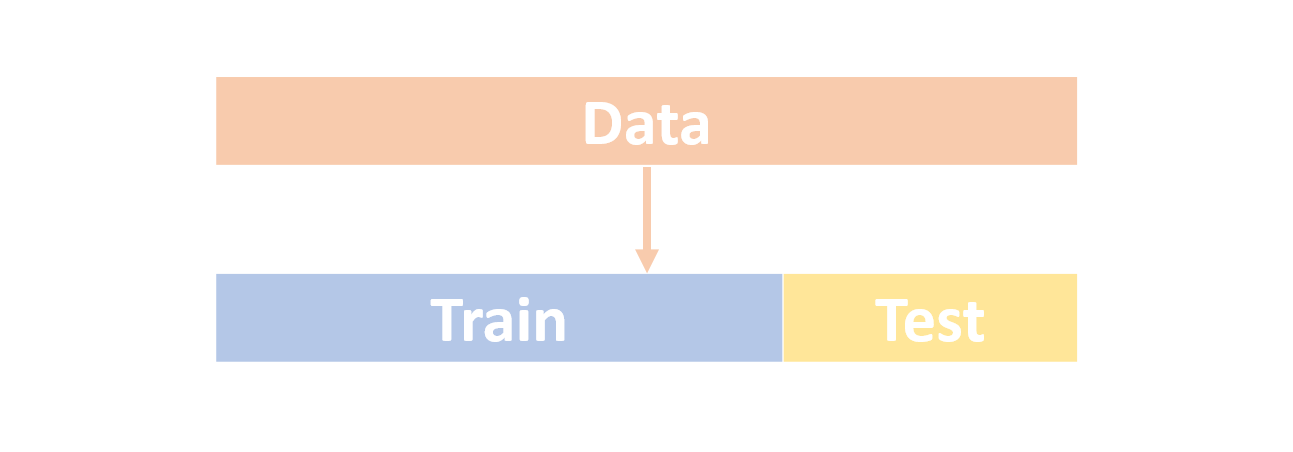
比例可能抓個 8:2
訓練的時候使用的是 Training Data,而後續再透過 Test Data 計算出一組 Test Loss 。
透過交叉比對 Train Loss 的曲線以及 Test Loss 的曲線可以觀察到是否有 Overfitting 的問題。
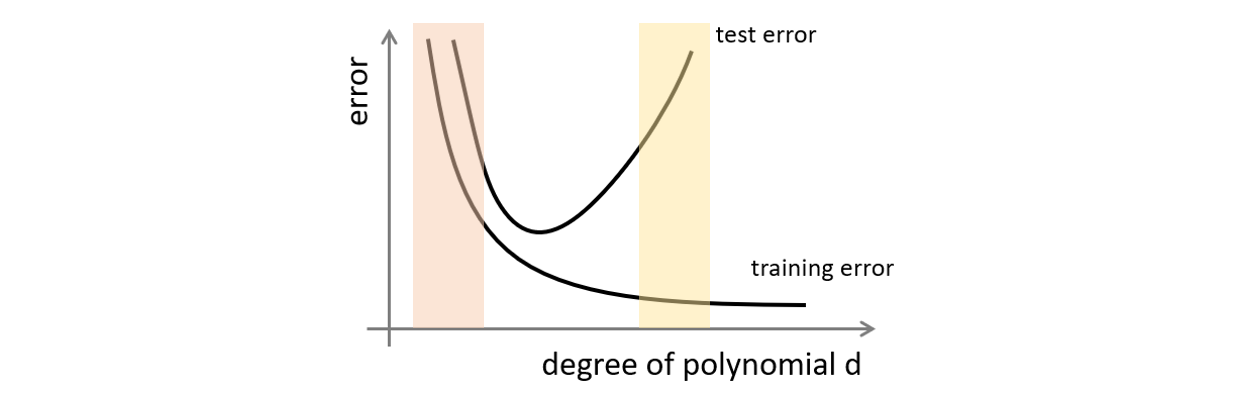
圖片修改自 2014 年 Andrew Ng Machine Learning 課程簡報
以圖像化的方式描述的話,如果現在落在紅色區域,那是 Underfitting。而在黃色區域則是 Overfitting。
小補充
有時候我們會用不同的術語描述 Overfitting 和 Underfitting。
Variance 描述 精度 , Bias 描述 準度 。
你可能打靶可以有很高的精度,卻都是打在紅心以外的固定位置。
你也可能打靶可以有很高的準度,即便不是每次都正中紅心。
依據精度與準度的不同你可以分成四種狀況

前面的做法聽起來十分合理,不過有個上面的做法後你會怎麼調整你的模型呢?
欸,沒錯!訓練的時候用 Training Data,訓練結束後拿 Test Data 去看有沒有問題。
這意味著,如果你發現了問題,那你就會去修正你的模型。
這會有什麼問題呢?
這會導致你在訓練模型至始至終都是用你有的全部資料去驗證模型的準確率和對現實資料的準確度。最終 你得到的模型會盡全力 fit 你的 Dataset 。
所以更多時候我們會把資料切成三個部分, Training Data 、 Test Data 以及 Validation Data 。
訓練時同樣以 Training Data 訓練,用來檢查的也只有 Test Data。你可以盡全力讓你的模型在 Training Data 和 Test Data 都有很棒的表現,不過最終最終你會是 以 Validation Data 計算準確率(驗證) 。
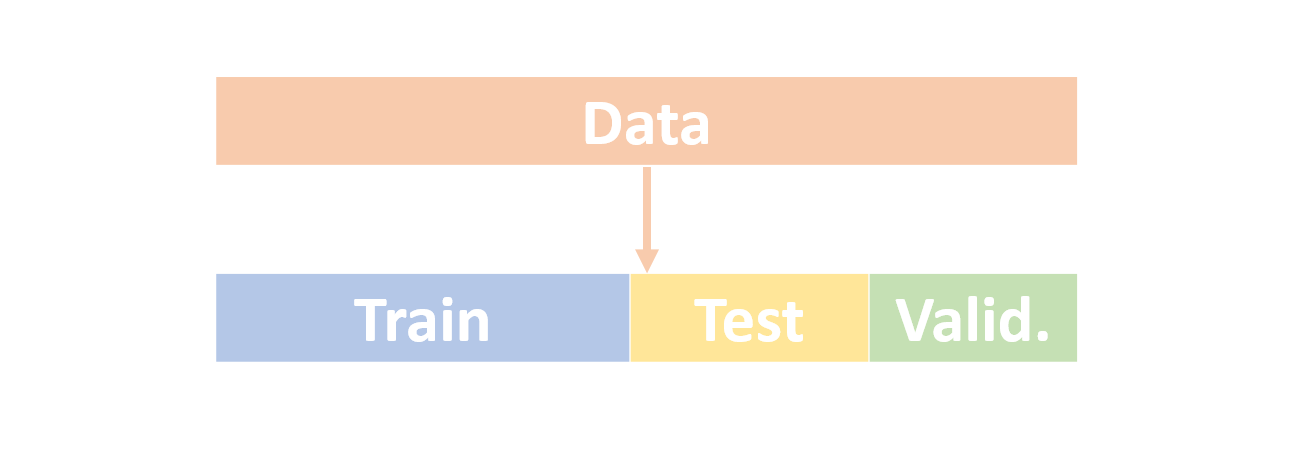
比例可以抓個 6:2:2
如此一來你既可以偵測模型是否 Overfitting,也可以避免模型僅僅只是在 Dataset 做得很棒而已。
切割成三種資料的做法通常可以得到足夠好的成果了,不過偶爾你會面臨到 資料切得不夠好 的問題。也許是切出來的 Train 和 Test 不夠泛化,導致模型無法好好訓練。也有可能是因為 Validation 切得不好,導致無法好好評估一個模型的好壞。
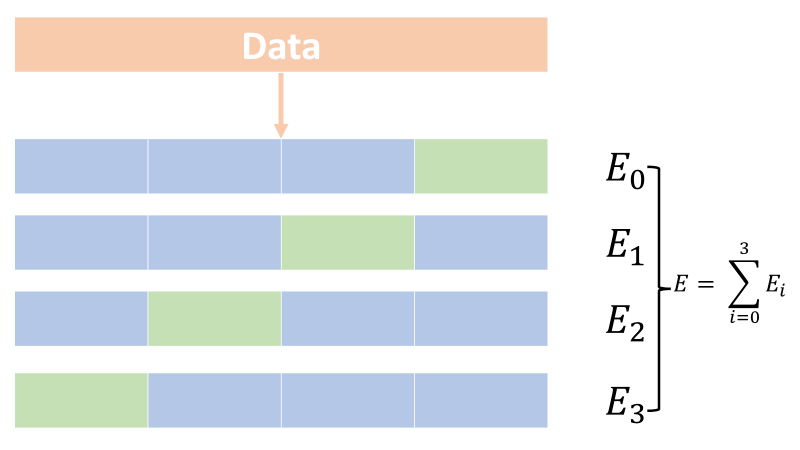
所以另一種常見的做法是把資料切成 K 等分,其中一等分用於 Validation,剩下拿去 Train。每次 Train 完之後會拿到一個 Validation Error。
接下來從 K 等分中選擇尚未被選擇過得當成 Validation,其他當成 Train,重複這個步驟下去,最終你會得到 K 組 Validation Error。
把這個 Validation Error 取平均,就可以避免切割時切得不夠好的問題。
今天用比較少的篇幅,主要 Focus 在透過切割資料集了解模型是否出現 Overfitting 的狀況,並且透過多切割 Validation Data,可以避免模型只在 Training Data 上做得很好,但是面對沒看過的資料有很低的泛化能力。最後也透過 K-fold Cross Validation 避免在切割上做得不好的狀況。
已經知道了 Overfitting 是什麼、什麼狀況下會出現 Overfitting、如何判斷 Overfitting 之後,下一步就是要決定如何針對這些問題做出修正。下一篇我們會來討論討論這些解決方案。
